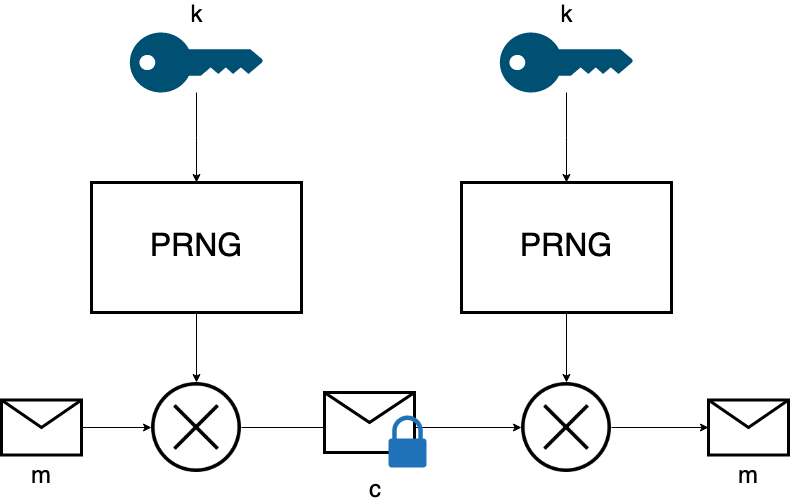
Teoría de la complejidad
Ciencia que estudia cuánto tiempo lleva resolver un problema al algoritmo más rápido posible
Criptografía: dado un mensaje cifrado con cierto algoritmo ¿existe un algoritmo más rápido que la fuerza bruta... aunque aún no sepamos cuál?
¿Cuánto tiempo tardarías en resolver este sodoku?
- Normas normales de Sudoku, y además...
- Las casillas separadas por movimientos de rey o caballo de ajedrez no pueden tener el mismo número
- Las casillas directamente adyacentes no tienen números consecutivos. Ejemplo: no hay un 6 encima, debajo, a la izquierda o la derecha de un 5 (en diagonal sí se puede)
- Pruébalo: The Miracle, de Mitchell Lee
- ¿Cuánto tiempo estimas que te llevará resolverlo?
- ¿Cuánto tiempo le llevará a un algoritmo que sea el más rápido posible?
Simon Anthony: "It might have a unique solution but it's not gonna be findable by a human being"
Hacer un algoritmo de fuerza bruta para un Sudoku es "sencillo": vamos comprobando números y, si funcionan, los dejamos
Eso se parece mucho a resolver por fuerza bruta un cifrado clásico
Pero estamos interesados en conocer el tiempo teórico que le llevará al algoritmo más rápido posible
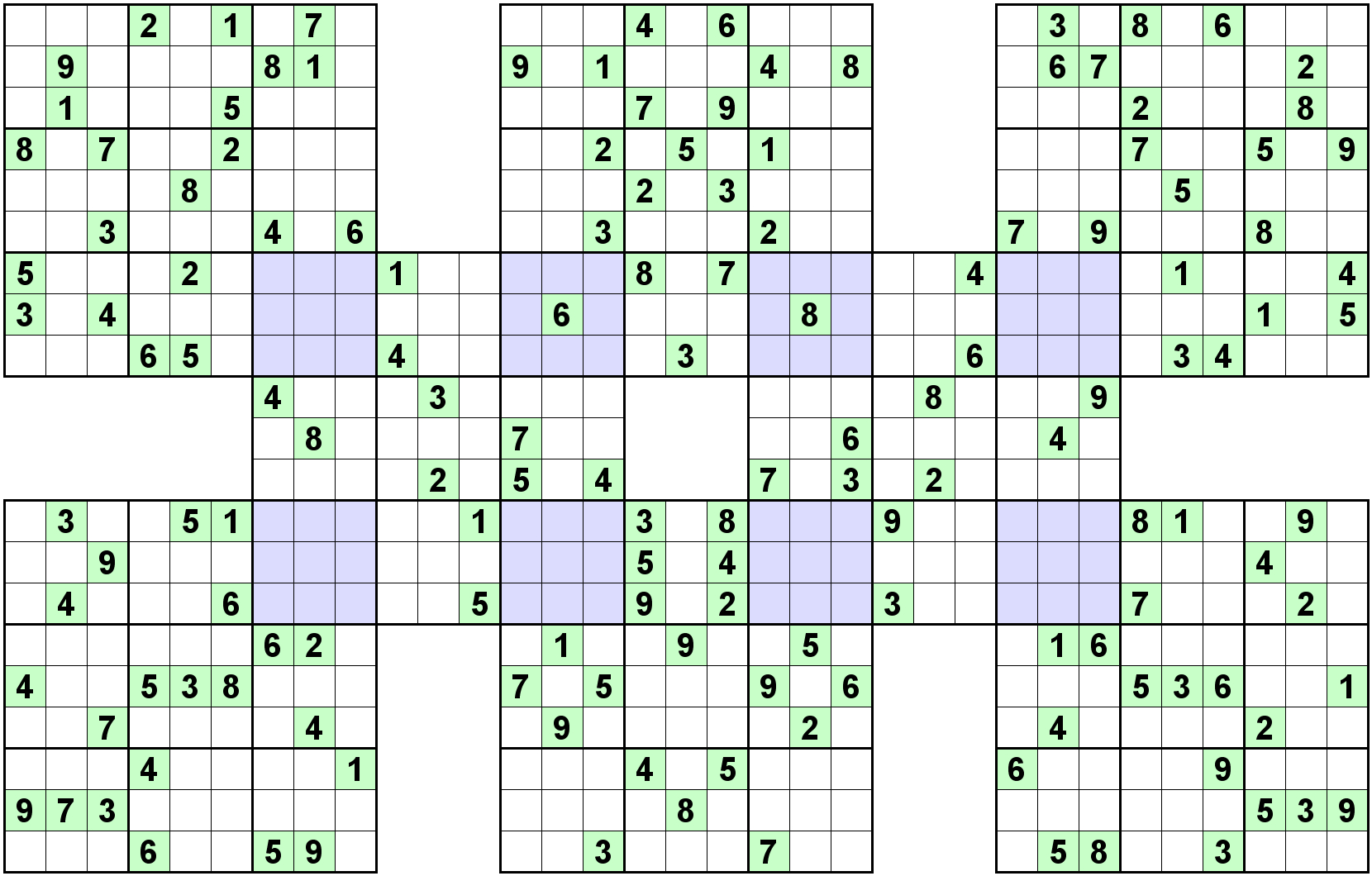
10 veces más casillas... ¿necesita 10 veces más tiempo? ¿ó 100 veces más tiempo? ¿ó 1000 veces más tiempo? ¿podremos acaso solucionarlo?
Si al aumentar el tamaño de un problema el tiempo necesario para resolverlo sigue siendo "razonable", decimos que es un "problema P"
¿Cuánto tiempo tardarías en comprobar si ésta es la solución?
Mucho tiempo para resolver, poco para comprobar
Existen algunos problemas que si aumenta el tamaño ya no podremos solucionarlos en un tiempo razonable
Pero si nos dan una solución, es muy rápido decidir si la solución correcta
Si lleva poco tiempo decidir si una solución es válida para un problema, decimos que es "un problema NP"
¿Cuánto tiempo tardas en colorear este mapa con 9 colores diferentes?
Transformación de problemas
- Si los el Sudoku y colores parecen similares, es porque lo son
- Se puede expresar un Sudoku como un problema de colorear mapas y viceversa
- Si podemos pasar rápidamente de un problema a otro y tenemos un algoritmo rápido para resolver uno, podemos resolver también el otro rápidamente
Si un problema NP se puede transformar en otro problema NP, entonces es un "problema NP-Completo"
Seguridad basada en problemas NP
Los matemáticos se han dado cuenta de que existen...
- Problemas P: se pueden resolver en un tiempo razonable
- Problemas NP: si te dan una solución, se puede verificar en un tiempo razonable. Fíjate: no sabemos si estos también se pueden resolver en un tiempo razonable
- Problemas NP-completos: se pueden convertir en otro problema que sepamos resolver en un tiempo razonable
A partir de ahora vamos a basar la seguridad en problemas:
- Que el criptoanálisis sea NP y por tanto probablemente no razonable
- Que sea corto decidir si algo es solución: el cifrado y descifrado es P y es razonable
Si además podemos convertir unos problemas en otros y sabemos que un problema es "computacionalmente seguro", el otro también lo será. Por tanto:
- El problema concreto en el que basemos la seguridad no importa siempre que sea equivalente a otro considerado seguro
- Escogeremos el problema que sea más sencillo de programar
Requisitos de New Directions in Cryptography, Diffie y Hellman, 1976. Hablaremos más de este paper en unos minutos
P = NP?
- Un problema P es también un problema NP, pero...
- ¿Todos los problemas NP son también P? ¿Y qué pasa con los NP-Completos?
- No sabemos si P es igual a NP, o si todos los problemas NP son NP-completos
- La seguridad actual se basa en la fuerte sospecha de que hay problemas NP que no son P ni NP-Completos
Definición formal: https://en.wikipedia.org/wiki/P_versus_NP_problem
¿Afecta a la criptografía?: https://security.stackexchange.com/questions/12802/how-will-security-need-to-be-changed-if-p-np
Ejemplos de problemas NP
- Sodoku, Colorear mapas, El problema del viajante...

- Logaritmos discretos, Factorizar números...
https://www.explainxkcd.com/wiki/index.php/399:_Travelling_Salesman_Problem
"Mucho tiempo": una definición
Hemos hablado de "tiempos razonables", "rápidamente" y "mucho tiempo"
... ¿podemos formalizarlo?
Cota superior asintótica: notación "big-O"
Escribimos que un algoritmo es de complejidad
Fíjate que
Lo importante es comparar las velocidades: ¿cómo crece el tiempo de ejecución cuando crece
¿Linealmente? ¿Exponencialmente?
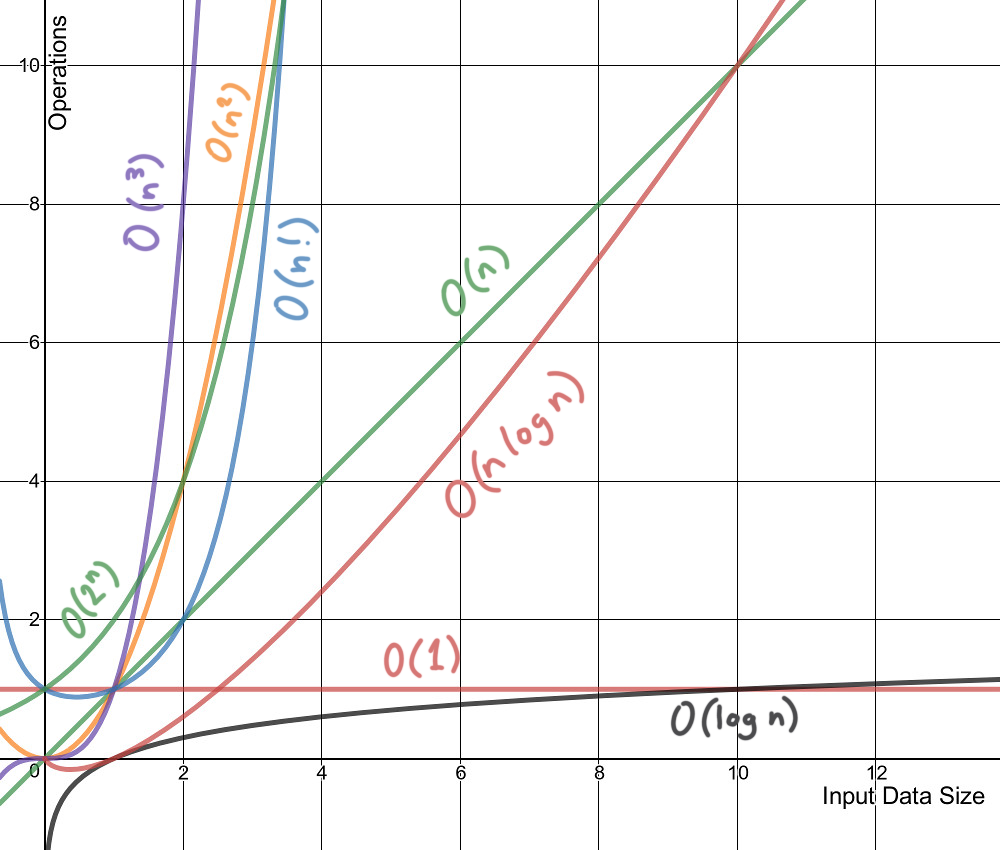
Fuente: https://laptrinhx.com/time-complexity-and-big-o-529699432/
big-O en criptografía
En criptografía,
Queremos algoritmos que el atacante necesite realizar
Pero también queremos que, conociendo la clave, el descifrado solo necesite
Un algoritmo está roto si el atacante necesita muchas menos de
Ejemplo: si queremos aumentar la seguridad de un algoritmo, pasamos de una clave de 128 a 256 bits
- Cifrado
- Mejor ataque posible
Nota que no necesitamos conocer el ataque: si se demuestra que el mejor ataque es de orden
"Tiempo razonable", la definición
Nota: las clases de problemas P, NP, NP-completo... en realidad se definen con notación big-O:
- P: problemas resolubles en tiempo polinomial
- NP: problemas comprobables en tiempo polinomial
Recuerda: un sistema es seguro computacionalmente si cualquier algoritmo probabilístico en tiempo polinomial solo puede romper el algoritmo con probabilidad negligible en
(falta definir eso de "probabilidad negligible", pero no lo haremos en este curso)
Problemas útiles en criptografía
- Factorización en números primos
- Logaritmo discreto
- Curvas elípticas: las veremos en el tema 5
Ejemplo: factorización en números primos
Es un problema NP y probablemente ni P ni NP-Completo
El algoritno conocido más rápido es GNFS:
Logaritmo discreto
Problema NP y probablemente no es NP-completo
Si conoces
Problema: encuentra
| 1 | 5 |
| 2 | 8 |
| 3 | 6 |
| 4 | 13 |
| 5 | 14 |
| 6 | 2 |
| 7 | 10 |
| 8 | 16 |
| 9 | 12 |
| 10 | 9 |
| 11 | 11 |
| 12 | 4 |
| 13 | 3 |
| 14 | 15 |
| 15 | 7 |
| 16 | 1 |
¿Cuánto vale
Gupo cíclico
La transparencia anterior muestra un ejemplo de grupo cíclico:
- Llamamos generador al número
El "aspecto" es el de una permutación pseudoaleatoria del cifrado de bloque, con
Dado un mensaje cifrado
Acuerdo de clave Diffie-Hellman
Diffie-Hellman
Método de acuerdo de clave simétrica (RFC2631, 1999)
New Directions in Cryptography, Whitfield Diffie y Martin Hellman en 1976
Primer algoritmo de criptografía asimétrica conocido y base de muchos de ellos
Lo estamos utilizando constantemente
Hipótesis DDH (Decisional D-H)
Problema: dado
Calcular
(Recuerda que
Pero si también nos diesen
Que nos den
Vamos a diseñar un protocolo entre Alice y Bob para que usen la clave
- El atacante solo conoce
- Pero Alice y Bob conocen también
Se asume que
Si lo necesitas, consulta la definición de Alice y Bob en el glosario
Protocolo D-H
Dos usuarios
- Acuerdan
- Escogen números en secreto
- Se envían entre ellos:
- Calculan en secreto:
- Y usan
Ejemplo sencillo:
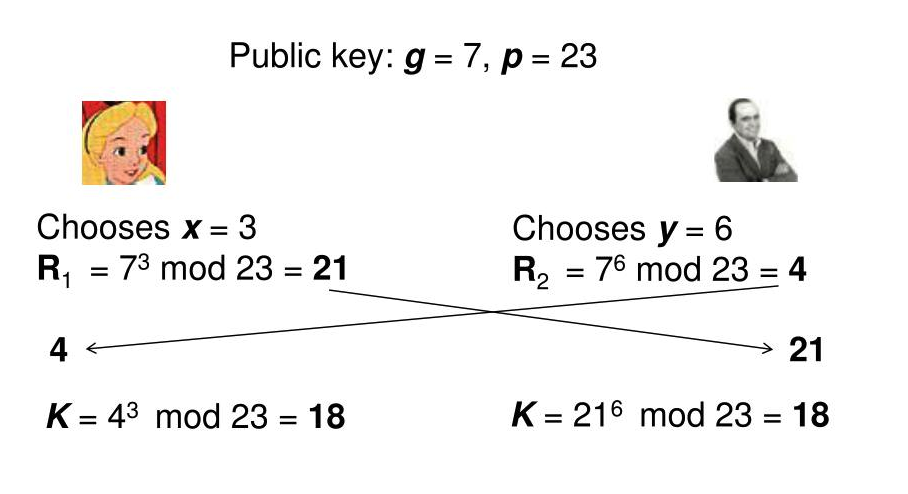
Aunque un atacante conozca
Claves secretas y claves públicas
- Alice y Bob acuerdan
- Cuando Alice y Bob se intercambian
Dado que el atacante (o cualquiera) conoce
| Paso 1 | Qué sabe Alice | Qué sabe Bob | Qué es público |
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | |||
| 4 |
Recuerda hipótesis DDH:
Alice y Bob, que no se habían visto nunca antes, puede utilizar
Llamamos:
- Claves de Alice:
- Clave pública:
- Clave privada:
- Clave pública:
- Claves de Bob:
- Clave pública:
- Clave privada:
- Clave pública:
Después del D-H ya no necesitan más estas claves y puede borrarlas...
... pero quedaos con el concepto, que lo usaremos dentro de poco
Selección de parámetros
D-H tiene cuatro parámetros: los secretos
"Paso 1: Alice y Bob acuerdan
La seguridad del algoritmo depende de que estos números estén bien escogidos
- Si no son primos entre sí o si
- Si
- Si
¡Estas son muchas condiciones! ¿Cómo podemos escoger
Afortunadamente no tenemos que escogerlos:
Ejemplo real:
p = 0xFFFFFFFFFFFFFFFFC90FDAA22168C234C4C6628B80DC1CD129024E088A6
7CC74020BBEA63B139B22514A08798E3404DDEF9519B3CD3A431B302B0A6DF25F
14374FE1356D6D51C245E485B576625E7EC6F44C42E9A637ED6B0BFF5CB6F406B
7EDEE386BFB5A899FA5AE9F24117C4B1FE649286651ECE45B3DC2007CB8A163BF
0598DA48361C55D39A69163FA8FD24CF5F83655D23DCA3AD961C62F356208552B
B9ED529077096966D670C354E4ABC9804F1746C08CA18217C32905E462E36CE3B
E39E772C180E86039B2783A2EC07A28FB5C55DF06F4C52C9DE2BCBF6955817183
995497CEA956AE515D2261898FA051015728E5A8AAAC42DAD33170D04507A33A8
5521ABDF1CBA64ECFB850458DBEF0A8AEA71575D060C7DB3970F85A6E1E4C7ABF
5AE8CDB0933D71E8C94E04A25619DCEE3D2261AD2EE6BF12FFA06D98A0864D876
02733EC86A64521F2B18177B200CBBE117577A615D6C770988C0BAD946E208E24
FA074E5AB3143DB5BFCE0FD108E4B82D120A93AD2CAFFFFFFFFFFFFFFFF
g = 2
Fuente: https://github.com/amiralis/pyDH/blob/master/pyDH/pyDH.py
Debilidades
¿Qué sucede si Malloy se pone en medio de un D-H?
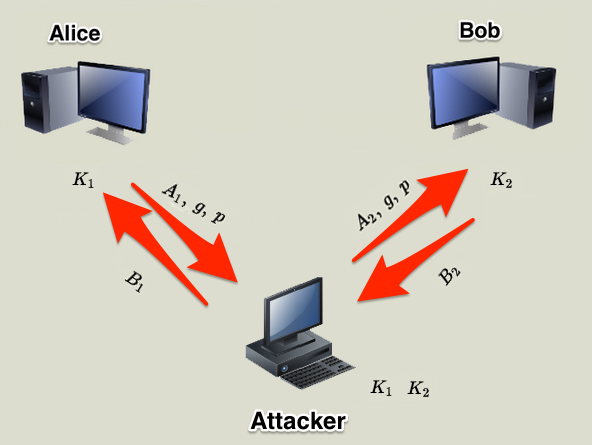
Alice y Bob están hablando en secreto... con el atacante
D-H necesita claves mucho más largas que AES:
Para acordar claves AES (que podemos aprovechar todos los números, primos o no) necesitamos una clave D-H (la
| AES (bits) | D-H (bits) |
|---|---|
| 128 | 3072 |
| 256 | 15360 |
NIST recomienda
Compara, para AES:
https://blog.cloudflare.com/why-are-some-keys-small/
https://www.keylength.com/en/3/
Uso de la clave D-H con AES o Chacha: Función derivación de clave KDF
El número secreto generado por el intercambio Diffie-Hellman no debe utilizarse como clave en protocolos de cifrado simétrico AES o Chacha ChaCha20: no es perfectamente uniforme
Se utiliza una transformación KDF (Key Derivation Function). Las KDF se pueden utilizar para extender claves en otras más largas o para obtener claves en un cierto formato. Las funciones de hash pueden usarse como KDF, aunque suelen incluir también inputs adicionales
Más información aquí:
Composición de elementos criptográficos
Acamos de ver una composición de elementos criptográficos: D-H y AES
- Alice y Bob acuerdan una clave AES-256 utilizando DH-4096
- Alice y Bob utilizan esa clave para comunicaciones seguras con AES.
Esto es solo una presentación de TLS. En la última parte de la asignatura veremos este protocolo con mucho más detalle.
Conclusiones
Resumen
- Hay una serie de problemas difíciles de resolver pero fáciles de comprobar: son los NP, en los que basaremos los demás sistemas que veremos
- La existencia de que estos problemas realmente son difíciles de resolver es una asunción de la criptografía actual. Amenaza: computación cuántica
- El problema del logaritmo discreto es uno de estos problemas y la base de muchos algoritmos
- D-H (en realidad, su actualizació para curvas elípticas "ECDH" que veremos en el tema 5) se utiliza para acordar una clave simétrica al inicio de una comunicación entre dos personas que no se conocen previamente
- Ahora tenemos claves divididas en dos partes: una parte es pública, la otra es privada
Referencias
- New Directions in Cryptography, Whitfield Diffie y Martin E. Hellman, 1976. El paper describe parte de la teoría de la complejidad que hemos estudiado aquí y describe el intercambio de claves Diffie-Hellman
- NP-Hardness, capítulo 12 del libro Algorithms de Jeff Erickson. Aunque no está enfocado a la criptografía, es una buena explicación de los problemas P y NP.