Criptografía Post-cuántica

Juan Vera del Campo - juan.vera@professor.universidadviu.com

Como decíamos ayer...

Fases de establecimiento de una sesión TLS (https). Cifrado híbrido:

  1. Autenticación de servidor mediante intercambio de certificados (criptografía asimétrica, RSA/ECDSA)
  2. Acuerdo de los parámetros de seguridad
  3. Establecimiento de clave compartida mediante criptografía asimétrica. Opciones: Diffie-Hellman o Encapsulación de clave (RSA, DSA)
  4. Cifrado simétrico de la comunicación AES/ChaCha con la clave anterior

La criptografía asimétrica es fundamental para establecer una conexión segura

La seguridad de la Criptografía asimétrica se basa en que no conocemos algoritmos rápidos para resolver problemas matemáticos como la factorización de números primos:

El algoritmo conocido para los computadores actuales es GNFS:

Factorizar este número con un computador actual lleva miles de años...

149802948092842184098210482184208402814092814092814902882314802
840182098201895139476316917369371469130591039583109734876139819
538591385031850135124214213434125103691373140750917604137601347
603176031760317603176136913701364316013860319760193760931707097
017436013760317460316703176031786136498314691376931763176931876
981376938176931876931769137693187613768713867136873187513769316
013463160316039187683714681397689713489671390486791837609138769
013876089317693187690137691374603918768931769137631769137691301
346871306871384761937693814708173468713689317693176814758134761
376134786139671396731467318967348769831476837639176913476931763
196731769317691384768931476831746083174687138671397613476317613
769347476138976831769831746983176731976913876091376891376981376
913476983174691347683476193769134769314769137693147691347691347
691387683147693147683148761364706946013746013681141213083928139

Pero... ¿y si existiesen otro tipo de computadoras que lo factorizasen en horas?

Hoy hablamos de...

  1. Computación Cuántica
  2. Criptografía Post-cuántica
  3. Ejemplo: ML-KEM
  4. Migración a criptografía post-cuántica
  5. Resumen y referencias

Computación Cuántica

Una introducción a vista de pájaro

Computación cuántica

  • La computación cuántica utiliza principios de la mecánica cuántica para realizar cálculos
  • Richard Feynman sugirió (~1980) que se podrían aprovechar comportamientos cuánticos para realizar cálculos de manera más eficiente que las computadoras clásicas
  • Ha sido un estudio solo teórico durante 50 años, pero ahora empezamos a poder construirlas

¿Qué es y cómo funciona la COMPUTACIÓN CUÁNTICA?

Q-bit

La unidad de la computación cuántica es el Q-bit, que puede existi en múltiples estados simultáneamente. 0 y 1 a la vez: superposición

Pueden empaquetar más información:

Intuitivamente: podemos aprovechar la superposición para probar muchas soluciones a la vez con un solo q-bit: trabajo en paralelo

Computación Cuántica: la Guía completa WIRED

Comparación con la computación tradicional

  • La computación cuántica permite resolver problemas complejos con una rapidez que no sabemos alcanzar con computación tradicional: supremacía cuántica
  • Cuidado: ¡no todos los problemas son complejos!
  • La computación cuántica da un resultado probabilístico. Es decir, "esto es una solución, probablemente"

¿Qué es lo que NO MEJORAN las computadoras cuánticas?

  • No traerán juegos con mejores gráficas
  • No nos traerán mejores aplicaciones informáticas
  • No traerán una Internet más rápida
  • Tardarán lo mismo en realizar la mayor parte de las tareas, pero son astronómicamente más caras

Es poco probable que tengamos una computadora cuántica en nuestros escritorios

La computación cuántica NO ES criptografía cuántica

  • La criptografía cuántica usa la física cuántica para crear un canal seguro
  • ¡No es necesario tener un computador cuántico para usar criptografía cuántica!
  • Ejemplo: distribución de claves cuántica (QKD)

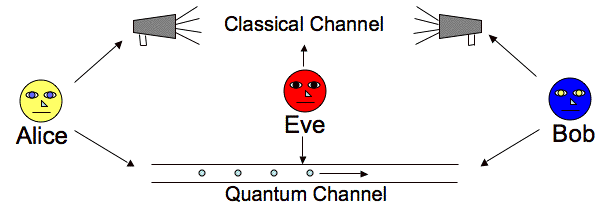
center

En esta clase no hablaremos de criptografía cuántica sinó de la post-cuántica, que definiremos más adelante

https://en.wikipedia.org/wiki/Quantum_cryptography

Entonces... ¿qué hacen las computadores cuánticas?

La computación cuántica permite ejecutar algoritmos de búsquedas más rápidamente que la computación tradicional

  • Entrenamientos de inteligencia artificial
  • Sistemas de optimización industrial
  • Sistemas de recomendación de compras y finanzas
  • Resolve los problemas matemáticos en los que se basa la criptografía actual mucho más rápido de lo esperado

Top 20 Quantum Computing Use Cases & Applications in 2024

Recordatorio: la seguridad actual está basada en la fuerza bruta

  • AES-128: fortaleza 128: hay que probar claves para encontrar la clave válida
  • Crecimiento exponencial de la fortaleza:
    • Aumentar 1 bit el tamaño de clave dobla el número de claves a probar
    • Aumentar 2 bits, número de claves x4
    • Aumentar n bits, número de claves x
  • En RSA, el equivalente son claves públicas de 2048 bits
  • ¿Aumenta la potencia de los PCs? No pasa nada, aumentamos el tamaño de la clave
  • Pero esto no nos sirve con computación cuántica: la dificultad de la fuerza bruta ya no crece exponencialmente con el tamaño de la clave

Algoritmos ejecutados por computadoras cuánticas

Algoritmos de interés para criptogafía:

Estos algoritmos tienen el potencial de romper la criptografía que estamos utilizando actualmente

Cuando tengamos un computador cuántico... ¡los malos ya sabrán usarlo!

Algoritmo de Grover

Búsqueda exahustiva en una secuencia no ordenada con mejora cuadrática.

Efecto: "raíz cuadrada de tiempo" de los algoritmos clásicos. AES-128 en

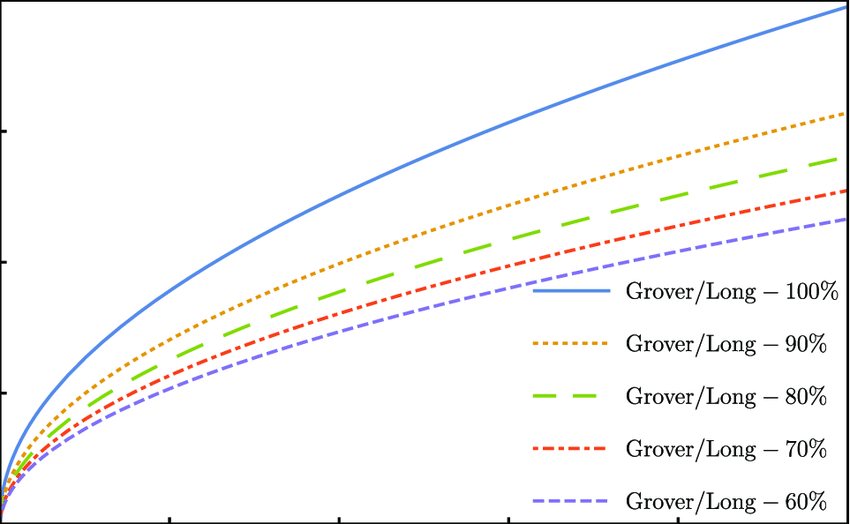
center

El algoritmo de Grover debilita la criptografía de clave privada y hashes (AES, SHA256...) diviendo su fortaleza entre 2

https://www.researchgate.net/figure/A-comparison-of-Grover-Long-algorithm-with-different-success-rates-1-d-2-The-query_fig3_356928043

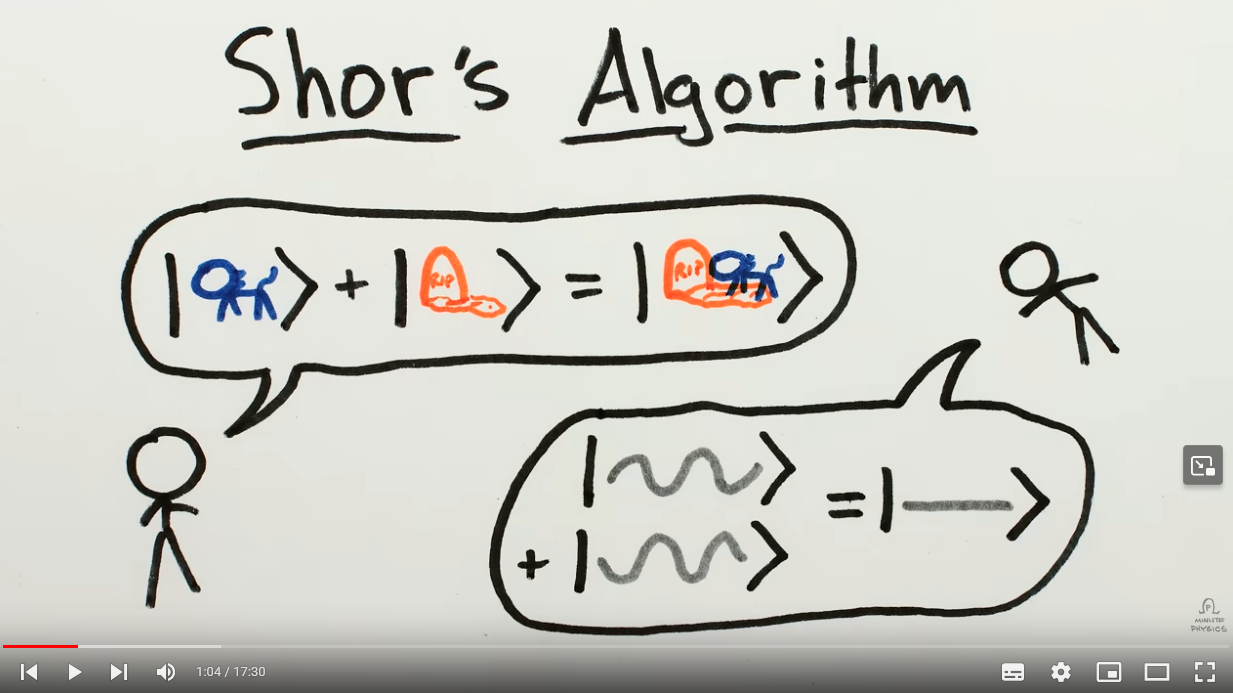
Algoritmo de Shor

Permite encontrar factores de un número de una manera eficiente. RSA, ECC y D-H en

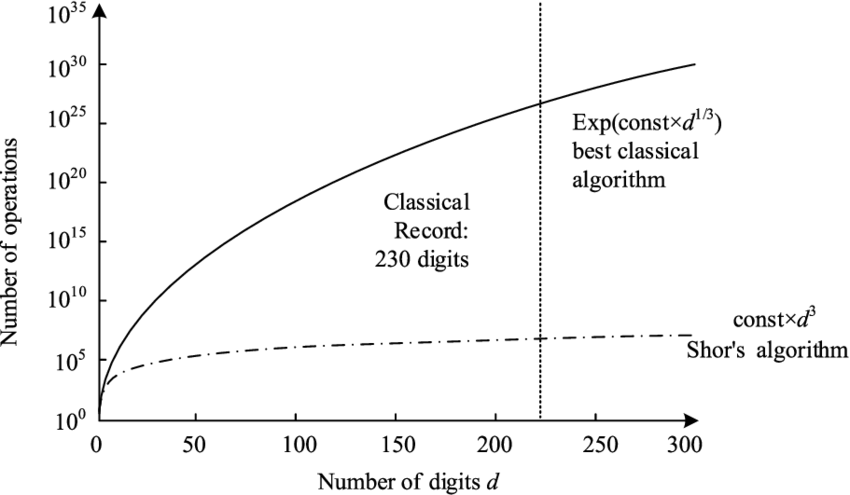
center

El algoritmo de Shor rompe la criptografía de clave pública (D-H, RSA...)

https://www.researchgate.net/figure/Shors-algorithm-has-exponential-acceleration-effect-compared-with-classical-algorithm_fig1_359643607

center

How Quantum Computers Break Encryption | Shor's Algorithm Explained

Inconvenientes de las computación cuántica

  • Solo mejora algunos problemas, otros los calculará tan rápido como la tradicional
  • Es muy cara
  • Decoherencia: un qbit es muy sensible al entorno y puede perder sus propiedades cuánticas
  • Muchos qbits hacen el sistema inestable
  • Necesitan temperaturas cercanas al cero absoluto
  • La respuesta es probabilística: probabilidad de error
  • No se ha demostrado que haya supremacía / ventaja cuántica

What Are The Remaining Challenges of Quantum Computing? Matt Swayne. March 24, 2023

Supremacía/ventaja cuántica

Demostrar de forma práctica que un computador cuántico puede resolver un problema más rápidamente que un computador tradicional

Cada poco tiempo alguien anuncia que ha demostrado la supremacía cuántica... con condiciones 1, 2, 3

Pero aún no se ha alcanzado para los algoritmos de Shor o Grover

It’s been 20 years since “15” was factored on quantum hardware, Robert Davis. Enero 2022

¿Número más grande factorizado con computación cuántica?

  • En 2001, el número 15
  • En 2012, el número 143
  • En 2016, el número 200.099
  • En 2019, el número 1.099.551.473.989... pero usando computación tradicional para simplificar el problema a un tamaño manejable por los computadores cuánticos (3 qbits), y un número "con truco"
  • En 2024, el número 8.219.999... sin apoyarse en computación tradicional

Hay interés y dinero en demostrar la supremacía cuántica, toma cualquier noticia con precaución

Records for efforts by quantum computers Wikipedia
Chinese Scientists Report Using Quantum Computer to Hack Military-grade Encryption The Quantum Insider, Octubre 2024
How to Detect Quantum Bullshit Sabine Hossenfelder, Junio 2024

Estado actual

center

Es probable que se alcance la supremacía cuántica en un futuro cercano

Criptografía Post-cuántica

Efectos de la computación cuántica en criptografía clásica

Algoritmo Tipo Algoritmo Defensa
AES Simétrico Grover ⚠ Tamaño de claves x2
SHA2 Función de hash Grover ⚠ Tamaño de salida x1.5
RSA Asimétrico, firmas Shor ☠ Rota, reemplazar
D-H Asimétrico, intercambio de claves Shor ☠ Rota, reemplazar
Elípticas ECDH, ECDSA... Shor ☠ Rota, reemplazar

Aunque no sepamos cuándo llegará el computador cuántico, ya tenemos que estar preparados y cambiar los algoritmos actuales

Criptografía post-cuántica

Algoritmos criptográficos que tendrán que usar las computadoras actuales/clásicas cuando existan las computadoras cuánticas

Observa:

  • Estos algoritmos criptográficos ya existen y sustituirán a RSA, ECDH o ECDSA
  • Los ejecutarán los computadores tradicionales, no las cuánticas
  • Los puedes usar ya en tus protocolos
  • Los tienes que empezar a usar antes de que llegue la computación cuántica

¿Cuándo tiempo nos queda?

center

En realidad, no nos queda tiempo: "Store now, decrypt later" 1, 2

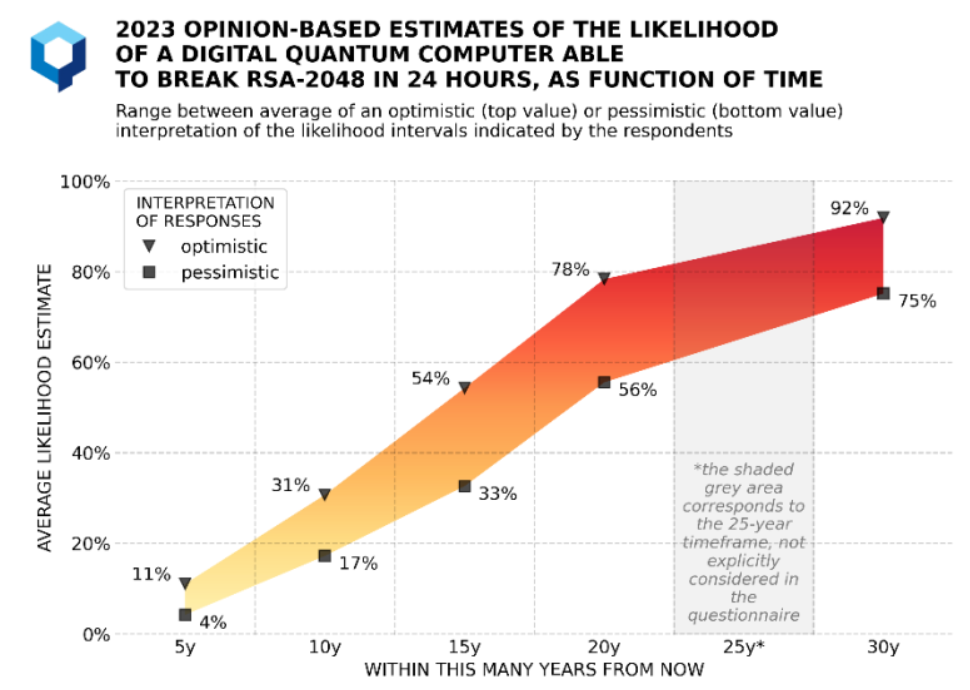
2023 Quantum Threat Timeline Report, Global Risk Institute, diciembre 2023

Problemas matemáticos en los que se basa la criptografía post-cuántica

  • Códigos correctores de errores
  • Retículos
  • Funciones de hash con y sin estado
  • Polinomios multivariantes cuadráticos
  • Isogenias definidas sobre curvas elípticas
Familia Ventajas Inconvenientes
Retículos Rápido y claves pequeñas Son muy nuevas
Isogenias Claves pequeñas, texto cifrado pequeño Muy lentas
Códigos Rápidas y texto cifrado pequeño, muy estudiadas Claves muy grandes
Basadas en hash Clve pequeña, muy estudiadas Firmas muy grandes, lentas
Multivariante Rápidas y claves privadas pequeñas Clave pública muy grande

Concurso del NIST

En 2016, el NIST (instituo de estandarización de EEUU), convocó un concurso para evaluar los mejores algoritmos post-cuánticos que le presentasen. Se centró en:

  • Mecanismos de encapsulación de claves o KEM (Key Encapsulation
    Mechanism    ), para sustituir a Diffie-Hellman
  • Firmas digitales, para sustituir a RSA

El NIST ya ha publicado (agosto de 2024) los estándares post-cuánticos:

  • ML-KEM: Module-Lattice-Based Key-Encapsulation Mechanism. FIPS 203. Estándar de intercambio de clave basado en CRYSTALS-Kyber. Reemplaza ECDH.
  • ML-DSA: Module-Lattice-Based Digital Signature Algorithm. FIPS 204. Estándar principal para firmas digitales post-cuánticas. Usa el algoritmo CRYSTALS-Dilithium. Reemplaza RSA, ECDSA
  • SLH-DSA: Stateless Hash-Based Digital Signature Algorithm. FIPS 205. Basado en Sphincs+. Es un "backup" para ML-DSA

https://www.linkedin.com/pulse/nist-releases-first-3-finalized-post-quantum-cryptography-fhpbe/

Algoritmos

Tipo Nombre Problema matemático Notas
KEM CRYSTALS-Kyber Retículo estructurado Seleccionado por el NIST: FIPS 203. Ahora llamado ML-KEM
KEM FrodoKEM Retículo no estructurado ⚠ Descartado por el NIST por lento, pero otras entidades aún lo recomiendan
KEM BIKE Códigos cuasi-ciclicos No presentado en tercera ronda, pero será evaluado
KEM HQC Códigos cuasi-ciclicos No presentado en tercera ronda, pero será evaluado
KEM Classic McEliece Códigos de Goppa ⚠ Clave demasiado grande
KEM SIKE Isogenias ☠ Roto con computación tradicional en 2022
Firma CRYSTALS-Dilithium Retículo estructurado Seleccionado por el NIST: FIPS 204
Firma Falcon Retículo estructurado ⚠ Descartado por el NIST
Firma SPHINCS+ Funciones de hash Seleccionado por el NIST: FIPS 205
Firma XMSS Funciones de hash ⚠ Descartado por el NIST por no ser general, pero recomendado para aplicaciones específicas

Comparativas

Comparativa con RSA-2048: intercambio de claves

Algoritmo Tamaño clave Tamaño cifrado Tiempo cifrado Tiempo KeyGen
Kyber512 x4 x4 x1 x4000

Comparativa con Ed25519 (ECDA): firmas

Algoritmo Tamaño clave Tamaño cifrado Tiempo firmado Tiempo verificar
Dilithium2 x40 x40 x5 x0.5
Falcon512 x30 x10 x8 x0.5
SPHINCS+128 x1 x100 x500 x7

Observa: buscamos las curvas elípticas para conseguir una criptografía asimétrica eficiente, y los nuevos protocolos son aún más ineficientes

Fuente: charla "Criptografía postcuántica: presente y futuro" de Adrián Ranea en Jornadas CCN-CERT 2023

Ejemplo: ML-KEM

Module-Lattice-Based Key-Encapsulation Mechanism. FIPS 203

ML-KEM (CRISTALS Kyber) - FIPS 203

  • Nombre oficial: Module-Lattice-Based Key-Encapsulation Mechanism
  • Nombre común: CRISTALS Kyber
  • Mecanismo de encapsulación de clave: dos personas que no se han visto nunca pueda tener una clave común que luego usarán en AES (o similar)
  • "Sustituto" postcuántico de Diffie-Hellman / ECDH
  • Basado en el problema "Aprendizaje con errores"

CRYSTALS-Kyber. Roberto Avanzi, Joppe Bos, Léo Ducas, Eike Kiltz, Tancrède Lepoint, Vadim Lyubashevsky, John M. Schanck, Peter Schwabe, Gregor Seiler, Damien Stehlé. Agosto 4, 2021
Learning with errors: Encrypting with unsolvable equations Chalk Talk, 2023. Explicación sencilla
CRYSTALS Kyber : The Key to Post-Quantum Encryption, Udara Pathum, 2024. Explicación completa

Aprendizaje SIN errores

  • Observa que se usa también la aritmética del módulo
  • Es un sistema lineal y dada la clave pública cualquiera podría sacar la privada

Aprendizaje CON errores

  • Observa que ahora hemos introducido ligeros errores en la igualdad. Por ejemplo, la primera ecuación resulta en 8 en vez de 11
  • Ya no es un sistema lineal y obtener la clave privada a partir de la pública no es fácil, ni siquiera para un computador cuántico

Cifrado y descifrado

  1. Cifrar un 0: el emisor escoge varias ecuaciones de la clave pública al azar y las suma (recuerda: mod 89)

  2. Cifrar un 1: el emisor escoge varias ecuaciones de la clave pública al azar, las suma y añade 44 (recuerda: mod 89, 44 es la mitad de 89)

  3. Descifrar un 0: el receptor sustituye los valores de su clave privada y comprueba si el error está "cerca" de 0

  4. Descifrar un 1: el receptor sustituye los valores de su clave privada y comprueba que si el error está "cerca" de 44

El receptor descifra "0" si el error está cerca de 0 y "1" si el error está cerca de la mitad del módulo. Hay una pequeña probabilidad de que el error sera mayor que la mitad del módulo y el descifrado sea incorrecto

Uso y comparación de D-H

  • De esta manera, bit a bit, un emisor puede enviar qué clave AES se utiliza el resto de la comunicación: encapsulación de clave
  • Valores reales: 256 variables, módulo 3329
  • Comparado con ECDH...
    • Hay una pequeña probabilidad de descifrar incorrectamente
    • Le lleva el doble de tiempo
    • El triple de procesado / energía
    • 70 veces más datos intercambiados
    • Clave de tamaño x4
    • Resistente a la computación cuántica

https://en.wikipedia.org/wiki/Kyber

Migración a criptografía post-cuántica

¿Qué tenemos que migrar?

  • Los mecanismos que firman firmware en los dispositivos físicos
  • Los mecanismos de intercambio de claves simétricas
  • Los mecanismos de firma digital
  • Cifrado simétrico: doblar el tamaño de la clave

The state of the post-quantum Internet, Bas Westerbaan. Marzo 2024

Tiempo de transición

  • Aún no existe una computadora cuántica con la potencia suficiente como para romper RSA, ni se sabe cuándo la tendremos: Quantum threat timeline report
  • Existe una "carrera cuántica" que están llevando China, USA, Europa por ser los primeros en tener una tecnología útil
  • Problema: store now, decrypt later
  • Históricamente, las transiciones son lentas: 3DES, MD5, TLSv1 aún están entre nosotros más de una década después de que no se recomiende su uso
  • Ya sabemos qué algoritmos post-cuánticos vamos a utilizar

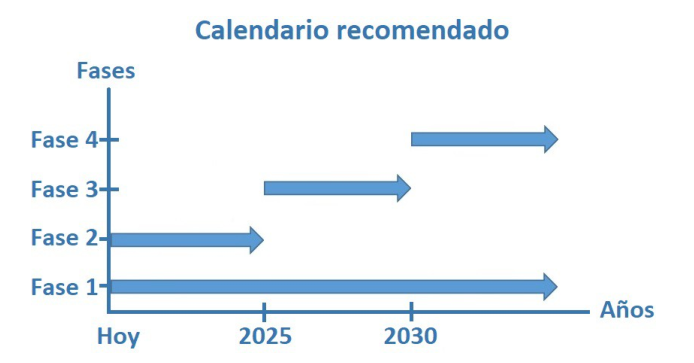
center

La recomendación es empezar ya con la transición

Recomendaciones para una transición postcuántica segura. CCN-TEC 009. Diciembre 2022

Retos de implementación

  • Los nuevos algoritmos no están soportados por sistemas antiguos: servidores, clientes, hardware...
  • No son tan eficientes como los algoritmos clásicos
  • Los nuevos algoritmos son más complejos, y eso también significa que son más difícil de implementar y proteger
    • Retículos: pequeña probabilidad de fallos en el descifrado
    • Retículos: necesitan generadores aleatorios gaussianos
    • FALCON: aritmética en coma flotante
    • BIKE: descifra en tiempo variable
    • XMSS: necesita guardar estado entre firmas

Esquemas híbridos

Mientras implementamos la criptografía post-cuántica completa podemos usar esquemas híbridos

  • Hash: incluir dos valores, hash tradicional y post-cuántico
  • Firmas: incluir dos firmas, firma tradicional y post-cuántica
  • KEM: cascada de funciones de derivación de clave clásicas, post-cuánticas

https://xiphera.com/hybrid-models-connect-the-post-quantum-with-the-classical-security/

Plan de migración

  1. Determinar la información que debo proteger y hasta cuándo.
    • Cifrado: largos periodos
    • Firma: hasta caducidad de certificado (unos 2 años)
  2. Realizar un inventario exhaustivo de productos y cifradores que empleo para proteger mi información y mis activos.
  3. Analizar si tales productos y cifradores son o no resistentes a la computación cuántica.
  4. Establecer un plan de migración a las soluciones híbridas
  5. Decidir qué nuevos productos necesito y cuánto tiempo requiero para su adquisición y despliegue.
  6. Determinar cuánto tiempo tengo disponible

Recomendaciones para una transición postcuántica segura. CCN-TEC 009. Diciembre 2022

center

No sabemos cuándo llegará la computación cuántica, pero ya podemos usar criptografía post-cuántica

Ejemplos de migración

AWS, Signal y otros ya permiten conectarse a sus servidores usando criptografía post-cuántica

Resumen y referencias

Resumen

  • La computación cuántica permite resolver ciertos problemas más rápidamente de lo que sabemos hacerlo con computación tradicional
  • Cuando llegue la computación cuántica:
    • AES, ChaCha, criptografía simétrica: deberá doblar el tamaño de las claves usadas
    • SHA, funciones de hash: deberán casi doblar los bits de salida
    • RSA, D-H, curvas elípticas, criptografía asimétrica, intercambio de claves y firmado: obsoleta, hay que buscar alternativas
  • Criptografía post-cuántica: sistemas criptográficos que usarán las computadoras clásicas para protegerse de las hipotéticas computadoras cuánticas
  • Agosto de 2024: el NIST ya ha estandarizado los algoritmos post-cuánticos que recomienda, y se espera que el resto de agencias tengan opiniones similares
  • No sabemos cuándo llegará la computación cuántica, pero ya podemos usar criptografía post-cuántica
  • El periodo de transición puede ser muy largo y se recomienda empezar ya la migración a criptografía post-cuántica

Referencias

Criptografía post-cuántica:

Generales sobre computación cuántica:

¡Gracias!

Una clave pública RSA tiene entre el doble y el cuadruple de esta longitud

Nota: no pretenderé explicar cómo funciona la computación cuántica, sinó cómo afectará a la criptografía del futuro próximo

Recordatorio: "problema complejo" no significa necesariamente problema difícil. Hay una rama de las matemáticas que estudia los problemas complejos, y tienen que ver con cuánto aumementan los recursos necesarios para resolver un problema (tiempo, memoria = dinero) cuando aumenta el tamaño del problema. Por ejemplo, factorizar números primos es un problema complejo. No porque sea difícil (no lo es), sino porque el tiempo necesario para factorizar un número aumenta exponencialmente con su tamaño Si un problema no es complejo, utilizar computación cuántica para solucionarlo en "matar moscas a cañonazos" Por eso es poco probable que veamos computadoras cuánticas en nuestros hogares: en nuestra vida diaria no necesitamos resolver problemas matemáticamente complejos

La criptografía cuántica utiliza los principios cuánticos para crear un canal de comunicaciones seguro. ¡No se necesita una computadora cuántica para usar la criptografía cuántica En el ejemplo, se usa un canal cuántico para distribuir una clave criptográfica tradicional que se puede usar, por ejemplo, para AES. En un canal cuántico, "el acto de medir cambia lo que se mide" (principio de incertidumbre), así que Alice y Bob se darán cuanta si hay alguien escuchando el canal, y no usarán esa clave para cifrar En esta clase no hablaremos de criptografía cuántica

En la imagen, IBM-Q quantum computer en la conferencia Supercomputing 18 de Dallas, Texas Para pensar: ¿realmente necesitamos resolver algoritmos de optimización tan rápido? ¿No nos valen los algoritmos tradicionales?

Observa: ya teníamos algoritmos antes de tener el primer computador cuántico!

Fíjate: da igual que aumentemos el tamaño de la clave, llega un momento en que resolver RSA se vuelve casi constante, independientemente de cuántos bits tenga la clave

El vídeo contiene detalles físicos y matemáticos de cómo funciona en algoritmo de Shor en sistemas cuánticos y es razonablemente sencillo

Sabemos que la computación cuántica es posible. Ahora, ¿es realmente más rápida que la tradicional? El consenso en la comunidad científica es que sí, que acabará teniendo ventaja/supremacía frente a la computación tradicional antes o después. Y tenemos que estar preparados para ello.

Fíjate: - son anuncios, no demostraciones - segutamente estos números estarán obsoletos cuando leas esto

Recuerda: - el cifrado simétrico (AES, ChaCha hash) se puede romper simplemente buscando qué texto original daría un cifrado. Eso es una búsqueda exhaustiva, y la computación cuántica puede hacer más rápidamente que la tradicional - La seguridad de RSA se basa en que no sabemos hacer factorización de números primos rápidamente con computadoras clásicas, pero sí que sabremos resolverlo muy rápidamente con computadoras cuánticas - D-H se basa en el problema del logaritmo discreto y tiene el mismo problema - Los sistemas de curvas elípticas también tendrán el mismo problema Aunque la criptografía simétrica resistirá, necesitamos sustituir la criptografía asimétrica

Fíjate bien: llamamos criptografía post-cuántica a la criptografía que ejecutarán las computadoras clásicas, no las cuánticas

EL intercambio de claves clásico podría hacerse acordando una clave (Diffie-Hellman) o simplemente enviando una clave simétrica cifrada con RSA. Esto último es lo que se llama "encapsulamiento de clave"

Todos estos algoritmos están bajo un estudio constante y se están descubriendo ataques existosos a algunos de ellos. Cada uno tiene ventajas y desventajas: manejo de estados, tiempos muy largos, claves largas...

A continuación vamos a explicar muy por encima en qué consiste el problema del aprendizaje con errores, dejándo detalles fuera. El primer enlace es la propuesta que se envió al NIST, el segundo enlace es una explicación sencilla en la que hemos basado esta sección, el tercer enlace incluye una versión más completa La intención de esta sección es introducir y entender aproximadamente en qué se basa este sistema, no entender todos los detalles

Imagen: https://blog.cloudflare.com/content/images/2022/10/image3.png

En la figura, esquema híbrido de generación de clave: la clave es una combinación de generación tradicional y post-cuántica

Para firmar las actualizaciones de firmaware se recomienda utilizar ya firmados post-cuánticos. El hardware puede estar funcionando durante décadas, muy posiblemente hasta después de que existan las computadoras cuánticas Los sitemas híbridos utilizan tanto criptografía cuánticas como post-cuántica, adaptando primero los algoritmos que puedan ser más sencillos (como D-H)