Requisitos para la confidencialidad perfecta
Tenemos confidencialidad perfecta si y solo si usamos un cifrado con las siguientes características:
- una clave tan larga como el mensaje
- totalmente aleatorio y no conocida por el atacante, ni siquiera en parte
- la clave no se usa nunca más
Durante 30 años, desde los años 40 a los 70, este sistema se conocía como one-time-pad, "libro de claves un solo uso", y era el más usado.
La confidencialidad perfecta no es práctica
Preferimos sistemas:
- Que usen claves pequeñas
- Que nos permitan resusar la misma clave
Un sistema así es imposible que sea perfecto, pero ¿puede ser lo suficientemente seguro?
Preferimos sistemas que, aunque puedan descifrarse, el atacante tenga que dedicar tantos recursos que no le sea práctico
Relajando la perfección
- Confidencialidad perfecta: a partir del texto cifrado no es posible deducir ninguna propiedad del texto en claro aunque el atacante tenga capacidad computacional infinita
- Confidencialidad computacional: a partir del texto cifrado no es posible deducir ninguna propiedad del texto en claro aunque el atacante tenga capacidad computacional razonable
Imagen: Nitin Jain, Birgit Stiller, Imran Khan, Dominique Elser, Christoph Marquardt & Gerd Leuchs (2016) "Attacks on practical quantum key distribution systems (and how to prevent them)". DOI: 10.1080/00107514.2016.1148333
Seguridad computacional
Seguridad computacional: un sistema es seguro computacionalmente si cualquier algoritmo probabilístico en tiempo polinomial solo puede romper el algoritmo con probabilidad negligible en
Informalmente: un atacante no puede descifrar el mensaje:
- ni juntando todo el dinero y la tecnología actual
- ...probablemente
- ...y quizá en el futuro sí se pueda
Con la seguridad computacional hay que definir el objetivo: "quiero un sistema criptográfico que mantenga este mensaje secreto durante los próximos 100 años"
La criptografía es una de las ramas más pesimistas de la ciencia. Asume la existencia de adversarios con capacidad ilimitada de ataque, los cuales pueden leer todos tus mensajes, generar información ilegítima o modificar tus claves aleatorias a su antojo.
Curiosamente, también es una de las ramas más optimistas, mostrando cómo incluso en el peor escenario inimaginable el poder de las matemáticas y la algoritmia puede sobreponerse a cualquier dificultad.
Alfonso Muñoz, Evasión de antivirus y seguridad perimetral usando esteganografía, 2021
Ataques de fuerza bruta
La criptografía computacionalmente segura permite
- Es un cifrado práctico: la clave es mucho más pequeña que el mensaje y por tanto es fácil de distribuir
- Pero si es muy pequeña, es posible hacer fuerza bruta: probar claves una a una hasta que encontremos la que es
Hay que usar un espacio de claves lo suficientemente grande como para que no sea posible hacer fuerza bruta hoy en día, y lo suficientemente pequeño como para que sea práctico
- podemos probar
- ó
- ó
- ó
- ó
- ó
Si tengo una "suerte media" sólo nos hará falta la mitad de las pruebas
Con hardware ad-hoc podemos llegar a multiplicar por
(
Fortaleza de un sistema de cifrado
El NIST recomienda (2020, sección 5.6.3) claves en las que un atacante
tenga que hacer
A partir del 2030 prevé recomendar que un atacante tenga que realizar
Fortaleza: números de pruebas (en bits) que tiene que hacer un atacante para descifrar un mensaje
Otras recomendaciones: https://www.keylength.com/en/compare/
Rompiendo algoritmos
Cuando la comunidad criptográfica rompe un algoritmo, se sustituye por otro
... pero es mejor prevenir: los algoritmos caducan y se cambian antes de que estén rotos
Un algoritmo está criptográficamente roto si se conoce un ataque más eficiente que la fuerza bruta
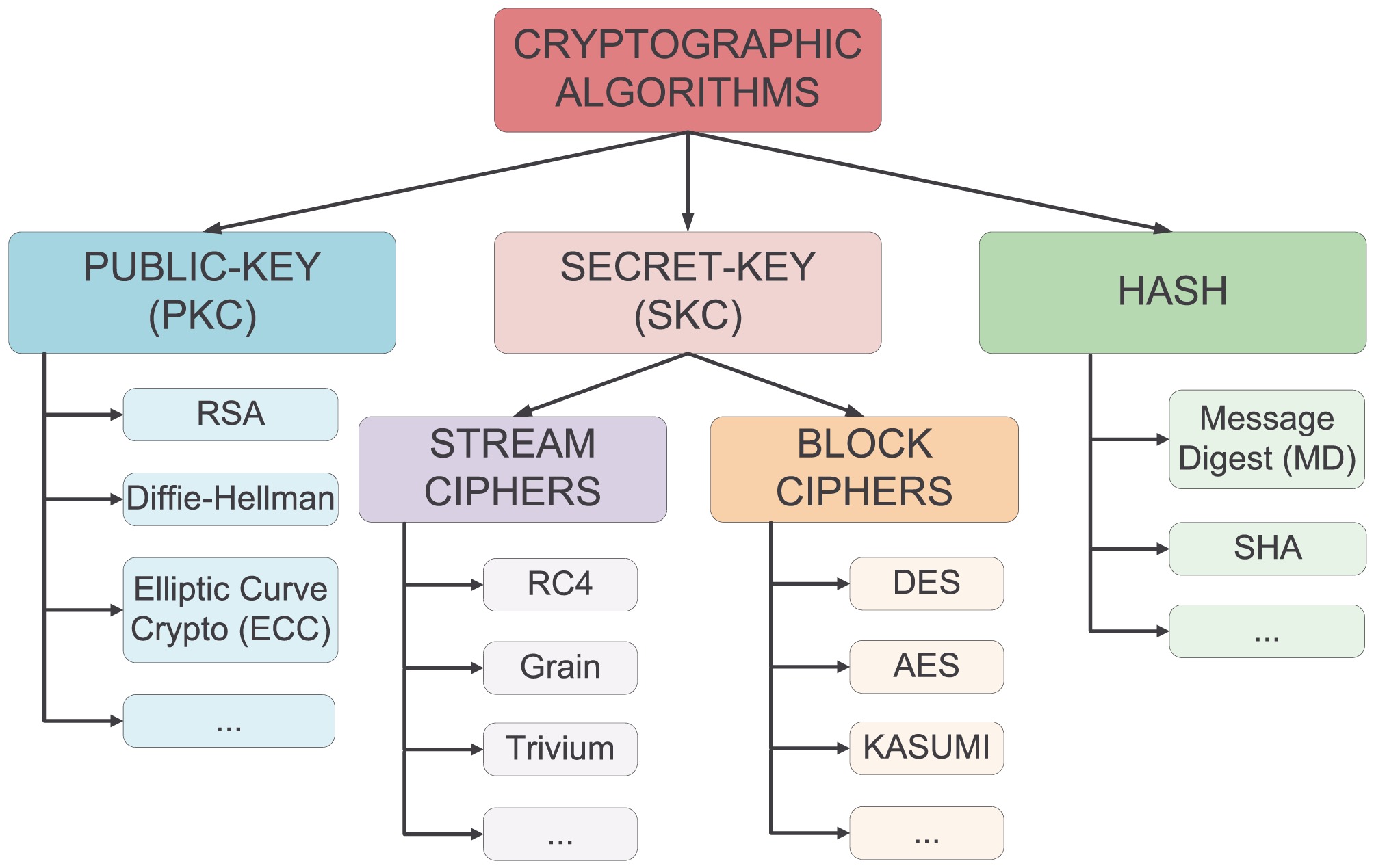
Criptografía simétrica / clave secreta
- Se usa la misma clave para cifrar que para descifrar
- Problema: ¿Cómo dos personas que no se conocen de nada acaban teniendo la misma clave?
- Usos: confidencialidad
Criptografía asimétrica / clave pública
- Existe una clave para cifrar, y una clave diferente para descifrar
- Problema:
- No supimos cómo hacerla hasta los años 70
- Es lenta y compleja
- Usos: autenticación, firma digital, intercambio de claves simétricas
Criptografía simétrica o de clave secreta
AES y ChaCha
Criptografía simétrica o de clave secreta
Usa la misma clave para cifrar que para descifrar
Ambas partes tienen que conocer la clave
¡Rapido y sencillo!
Ejemplos actuales: AES, ChaCha
Ejemplos rotos y obsoletos: RC4, DES, TDES
Fondo: https://www.pexels.com/photo/photo-of-person-using-magnifying-glass-7319077/
Criptografía simétrica: tipos
| Flujo | Bloque |
|---|---|
| Cifra un stream continúo de datos | Divide los datos en bloques, que se cifran separadamente |
| Más rápido | Más lento (a menos que exista ayuda del hardware) |
| Fácil de programar: pequeños dispositivos | Más complejo |
| Implementado en software | Implementado en hardware |
| RC4, ChaCha20 | 3DES, AES |
Cifrado de flujo
Basado en los bloques de una solo uso (one-time-pad)
Idea: crea una clave tan larga como el mensaje:
...a partir de una clave
para después hacer:
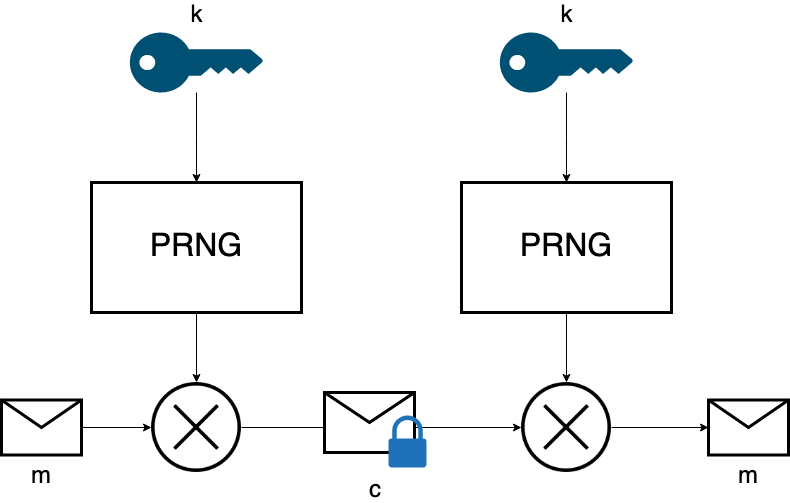
PRNG: Pseudo Random Number Generator
La seguridad del cifrado depende del generador PRNG utilizado...
...y de que nunca se envíen dos mensajes cifrados con la misma clave
(vamos a repetir esto muchas veces en el curso)
Lorenz SZ fue una máquina alemana de cifrado de flujo, rota porque un operador envió dos mensajes diferentes seguidos sin cambiar la clave.
¿Cómo hacer cifrado de flujo? Intento 1
Supongamos que tenemos una función PRNG, y usamos una clave k como semilla del PRNG para cifrar un flujo de datos en una conexión
Si ciframos dos mensajes cifrados
¡Un atacante puede hacer XOR de los dos textos cifrados y obtener el XOR de los textos en claro!
Nunca hay que usar la misma clave (ni generada) con dos mensajes diferentes
Información adicional: Chosen plaintext attacks
Intento 2
Generar variaciones de las claves en cada transmisión
Supongamos que la semilla no es directamente la clave, sino una función de la clave y otro parámetro
Y
Ahora la semilla "es diferente" con cada tranmisión
Pero tenemos que asumir que un atacante conoce
Nonce: number used only once
Curiosamente: ¡esto es correcto!: reservar algunos bits de la clave para un contador:
SESAMO_1, SESAMO_2, SESAMO_3...
Este elemento se conoce como nonce y forma parte de muchos algoritmos criptográficos
El cifrado de flujo es tan seguro como:
- La corrección de la hipótesis de que la función PRNG sea realmente PRNG
- El espacio de claves (de semillas) sea tan grande que sea improbable que un ataque de fuerza bruta sea factible
- Que se cumplan las hipótesis de uso:
- clave diferente en cada comunicación
- nonce y
Ejemplos
- RC4 (histórico): obsoleto
- ChaCha: derivado del Salsa20 y probablemente la única alternativa al AES en TLS 1.3
ChaCha es el algoritmo de cifrado simétrico de flujo más usado
Cifrado de bloque
Alternativa al cifrado de flujo: cortar el texto en claro en bloques de la misma longitud de la clave y cifrar cada uno de los bloques
El cifrado de bloque es el muy utilizado: es rápido, no necesita exigentes o lentos algoritmos PRNG y ya tenemos hardware especializado en su cifrado/descifrado
Modos de operación
Los cifrados de bloque se organizan como "modos de operación": como ordenamos las cajas de cifrados y descifrados.
Cada modo de operación tiene ventajas y desventajas según para qué queremos usar el sistema
Atención: hay un modo de operación que no debe usarse nunca
Si acumulamos estado durante el cifrado, podemos utilizar este estado sobre el cifrado del siguiente bloque:
- ECB: Electronic Code-Book,
- no debe usarse
- CBC: Cipher Block Chaining
- el bloque
- el bloque
- OFB: Output Feedback
- cifras el cifrado anterior, y el resultado
- cifras el cifrado anterior, y el resultado
- CTR: Counter
- cifras un contador, y el resultado
- cifras un contador, y el resultado
ECB: Electronic Code-Book
Fallo obvio: está usando la misma clave para cifrar mensajes diferentes.
Eso nunca se puede hacer.


No se debe usar un cifrado de bloque en modo ECB
CBC: Cipher Block Chaining
OFB: Output Feedback
CTR: Counter
Vector de Inicialización (IV)
Los distintos encadenados requieren de una semilla inicial para empezar el encadenado: vector de inicialización (IV), que cumple la misma función que un nonce.
Esto hace que en lugar de transmitir
- IV en CBC: es el hipotético bloque cifrado
- IV en OFB: es el bloque que se cifra constantmente
- IV en CTR: es el valor inicial del contador que se cifra ECB, y se aplica sobre los bloques en claro (con
AES_128_CTR es efectivamente un cifrado de flujo, siendo
Advanced Encryption System (AES)
Desarrollado por Vincent Rijmen y Joan Daemen (aka: Rijndael), que ganaron el concurso celebrado por el NIST para sustituir a DES en 2001.
AES (FIPS 197, 2001) es un cifrado de bloque:
- longitud de bloque: 128 bits (16 Bytes)
- longitud de clave: 128, 192 ó 256 bits
background: https://whatsupcourtney.com/wp-content/uploads/2017/10/Things-to-do-in-Leuven-52-e1560945504897.jpeg
Rendimiento
- AES-128: 1,1 Gbps (seguridad 128 bit)
- AES-192: 0,9 Gbps (seguridad 192 bit)
- AES-256: 0,7 Gbps (seguridad 256 bit)
- Salsa20: 3,2 Gbps (seguridad 256 bit)
- ChaCha20: 3,2 Gbps (seguridad 256 bit)
- AES "hardware": ~8 veces más rápido (Intel, 2011)
- DES: 250 Mbps (seguridad 56 bit)
- 3DES: 100 Mbps (seguridad 112 bit)
Comparación flujo y bloque
| Flujo | Bloque |
|---|---|
| Más rápido | Más lento (a menos que exista ayuda del hardware) |
| Fácil de programar: pequeños dispositivos | Más complejo |
| Implementado en software | Implementado en hardware, mucho soporte ya desplegado |
| RC4, ChaCha20 | 3DES, AES |
Problema del cifrado simétrico

El cifrados de flujo (ej. ChaCha) y de bloque (ej. AES) permiten enviar mensajes computacionalmente seguros
Solo necesitamos que las dos partes tenga una clave secreta en común
¿Cómo conseguimos que las dos personas que no se han visto nunca tengan una clave secreta común?
El protocolo de intercambio de claves Diffie-Hellman permitió por primera vez en la historia que dos personas cualquiera que no se conocían mantuviesen una conversación confidencial por medios dgitales...
...pero su artículo no se llamó "Solución al problema de intercambio de claves". Tenía un título mucho más ambicioso: Nuevas direcciones en la criptografía
¿Qué direcciones eran esas?
Foto: https://www.publicdomainpictures.net/en/view-image.php?image=363738&picture=signpost-giving-directions (CC0)
Criptografía asimétrica o de clave pública
Diffie-Hellman, RSA y curvas elípticas
Firmado digital de contratos
New Directions in Cryptography (Whitfield Diffie y Martin Hellman, 1976) exploraba qué se necesitaba para que dos empresas pudiesen firmar un contrato mercantil:
- Confidencialidad, sin tener una clave secreta común
- Autenticación de la identidad (llamada "autencidad de usuario" en el paper original)
- Integridad del contrato (llamada "autenticidad del mensaje")
- No repudio del contrato por ninguna de las partes
Es la lista que conocemos como "los servicios básicos de seguridad" (tema 1)
El primer punto, "confidencialidad", se resolvía con los cifrados que estaban apareciendo ese mismo año (DES)...
...pero se necesitaba intercambiar primero una clave simétrica
Propuesta: protocolo de intercambio de claves
Y se dieron cuenta: se puede extender la misma idea para solucionar todo lo demás
Criptografía asimétrica
También conocida como criptografía de clave pública
Cada persona tiene dos claves:
A veces son intercambiables: lo que se cifra con una se descifra con la otra
Compara con criptografía simétrica: misma clave para cifrar y descifrar, Bob y Alice tienen que manetenarla en secreto
Esquema de cifrado
- Todos conocen la clave
- Cualquier puede cifrar un mensaje para Bob, solo Bob puede descifrarlo: confidencialidad
Esquema de firma electrónica
- Solo Bob puede cifrar con su clave
- Pero si pueden descifrar el mensaje, todos saben que el mensaje solo puede haberlo enviado Bob: autenticación
Trap door functions, funciones trampa
Las matemáticas de la criptografía asimétrica utilizan funciones trampa:
- Si conoces
- Si conoces
No encontramos una función trampa hasta 1976
Problema del Logaritmo Discreto
Resuelve la
-
- Eso es fácil y se puede extender a cualquier problema similar:
- Si te dan
Para más detalles de este problema, consulta tema 4
Resuelve la
- Ten en cuenta:
- Solución:
- Si no has podido resolverlo, no es porque no tengas suficientes conocimientos... es que no sabemos hacerlo rápidamente: Problema del Logaritmo Discreto (DLP)
- ...pero calcular
- El DLP es una trap door function
Protocolo Diffie-Hellman: intercambio de claves simétricas
Utilizado para acordar una clave simétrica entres dos personas antes de las comunicaciones
Idea básica:
- Bob envía a Alice una parte de la clave simétrica que usarán, cifrándola con la clave pública de Alice.
- Alice envía a Bob una parte de la clave simétrica que usarán, cifrándola con la clave pública de Bob.
- La clave final es la combinación de ambas partes, que solo las conocen Alice y Bob
Dos usuarios
- Acuerdan
- Escogen números en secreto
- Se envían entre ellos:
- Calculan en secreto:
- Y usan
Observa: para que un atacante que solo conoce
Claves secretas y claves públicas
| Paso 1 | Qué sabe Alice | Qué sabe Bob | Qué es público |
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | |||
| 4 |
Alice y Bob, que no se habían visto nunca antes, puede utilizar
Nuevas direcciones
El DLP, en la versión D-H de 1976, no una solución completa: permite hacer acuerdo de claves, pero no cifrado
En pocos años aparecieron nuevas funciones basadas en esas ideas: RSA, ElGammal, DSA, Pailier...
Luego, las soluciones se refinaron con curvas elípticas: ECDH (Elliptic Curves Diffie-Hellman), ECDSA (Elliptic Curves DSA)...
RSA: claves públicas y privadas
Fue el primer método de cifrado conocido que usaba claves públicas y privadas
Sigue usándose en la actualidad
A method for obtaining digital signatures and public-key cryptosystems, Ron Rivest, Adi Shamir, Leonard Adleman, 1978
Está basado en la dificultad en factorizar números grandes
Background: https://hsto.org/getpro/habr/post_images/453/10e/602/45310e602d784a489301bf1996edef68.jpg
El protocolo RSA: generación de par de claves
- Escoge dos números
- Calcula:
- Calcula:
- Protocolo original:
- Versión moderna:
- Protocolo original:
- Escoge al azar
- Calcula:
- Claves:
- Se descartan
El protocolo: cifrado y descifrado
Cifrado: Para enviar un mensaje a Alice, obtengo su clave pública
Descifrado: Alice utiliza su clave privada
Velocidad de proceso
Para crear el par de claves hay que buscar:
- números muy grandes que sean primos (y otras condiciones):
- número muy grande
- inversos de un número entero:
Es decir: la elección de un par de claves es un proceso muy lento. Segundos, minutos, horas si las claves son grandes
A cambio: el cifrado y descifrado son relativamente rápidos comparados con otros sistemas de cifrado asimétrico
El cifrado asimétrico es muy lento comparado con cualquier proceso de cifrado simétrico
Tamaño de claves
Hemos visto que tanto Diffie-Hellman como RSA necesitan números primos
Los números primos están muy separados entre sí: el número de primos menores que
Ejemplo: hay
"Son pocos primos"
La criptografía asimétrica necesita claves mucho más largas que la criptografía simétrica
Fuente: https://en.wikipedia.org/wiki/Prime_number_theorem
Gráfico: https://en.wikipedia.org/wiki/Ulam_spiral
| Simétrica (bits) | RSA (bits) | D-H ( |
|---|---|---|
| 80 | 1024 | 1024, 160 |
| 128 | 3072 | 3072, 224 |
| 192 | 7680 | 7680, 384 |
| 256 | 15360 | 15360, 512 |
Es decir: para intercambiar una clave AES-256 aprovechando todos sus bits, necesitamos claves RSA de 15360 bits
Si usamos tamaños de clave RSA de 4096 bits (tamaño típico), podremos intercambiar una clave simétrica equivalente a AES-128
Curvas elípticas
Propuestas como trap door function en 1987 por Neal Koblitz y Victor S. Miller de forma independiente
- Ventaja: necesitan menos proceso y memoria, se pueden implementar en máquinas pequeñas: móviles, tarjetas inteligentes...
- Problema: teoría matemática compleja
Necesitan claves más cortas que la criptografía asimétrica basadas en DLP o RSAP para ofrecer una seguridad equivalente
Trap door function
Dado un punto
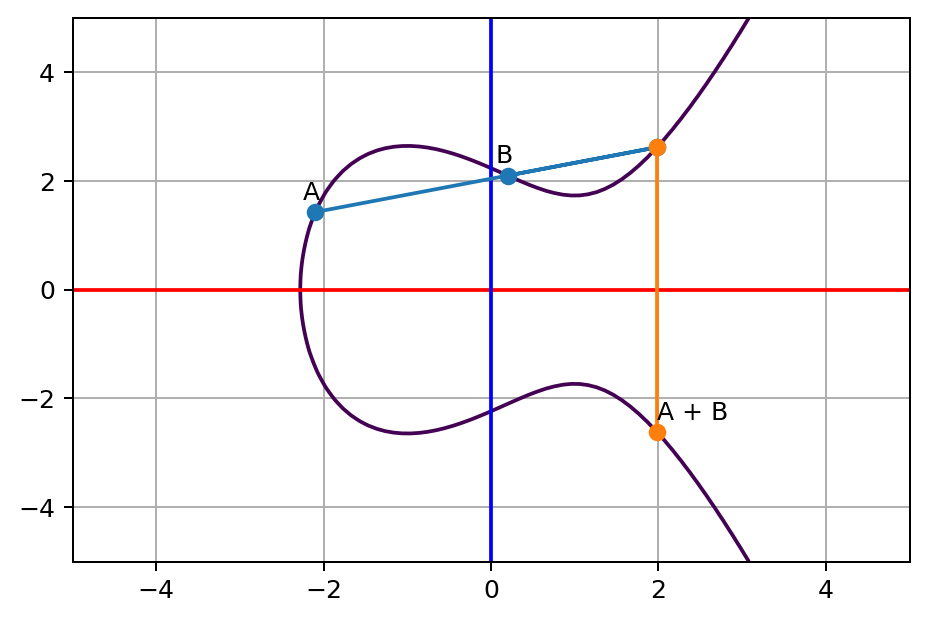
Usamos el símbolo "suma" por tradición, pero no es una "suma geométrica"
Y lo volvemos a aplicar, varias veces, desde el mismo origen
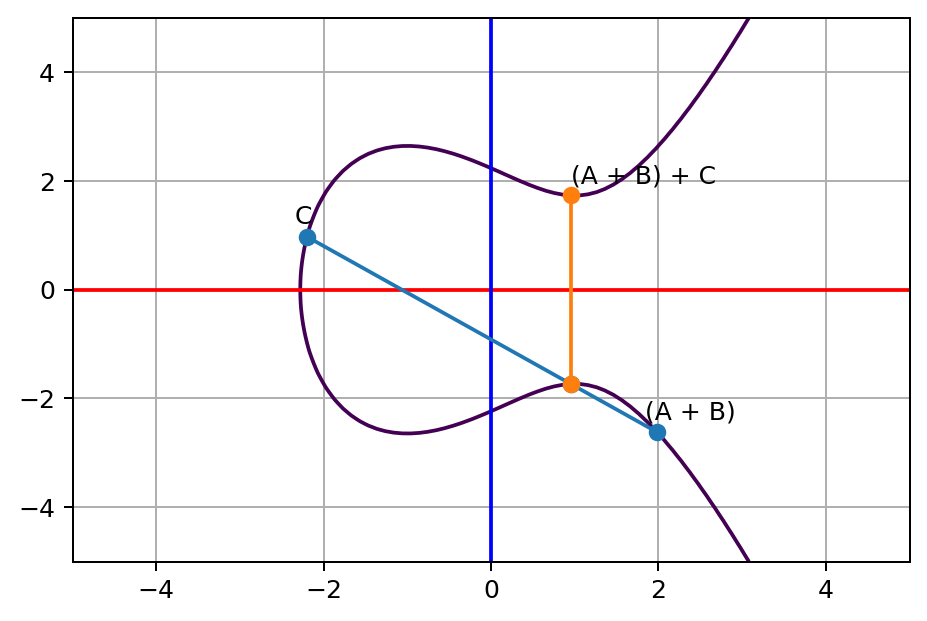
En vez de empezar con dos puntos, podemos empezar con uno solo, y la recta inicial es la tangente a la cura. El resto sigue igual
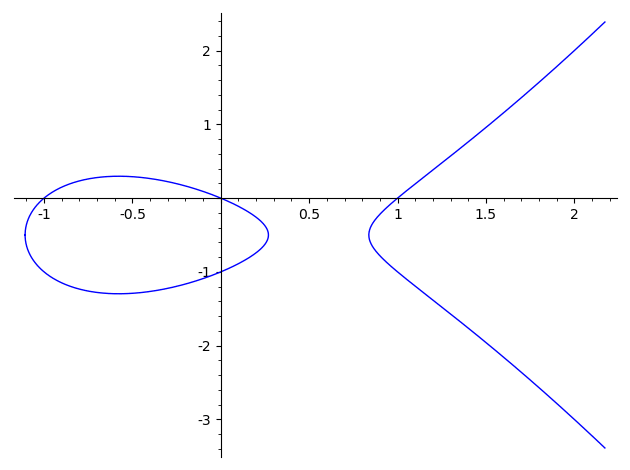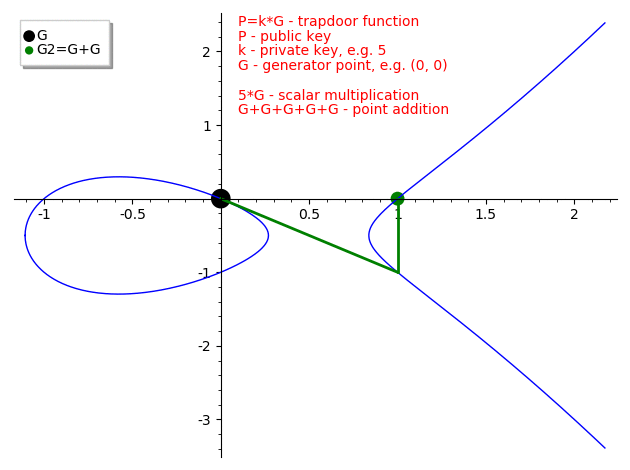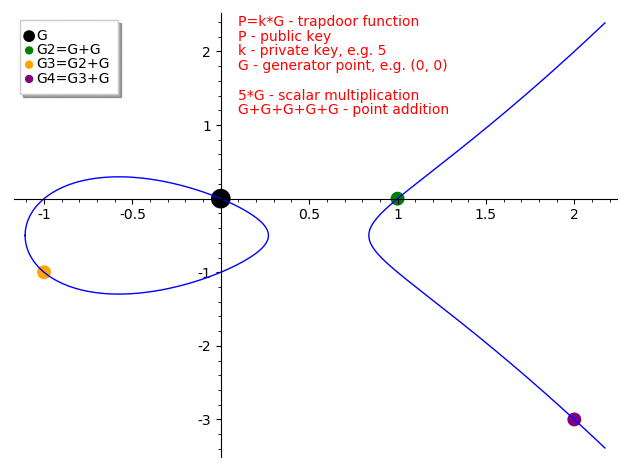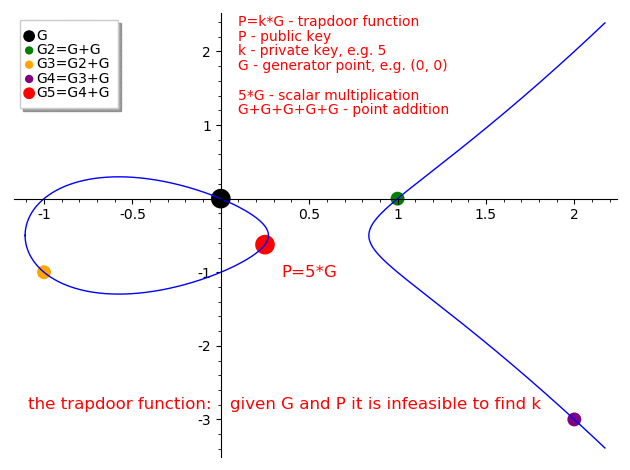
Fuente: https://medium.com/@icostan/animated-elliptic-curves-cryptography-122fff8fcae
Esta es la trap door function:
Es la aplicación de
Dado
Eso es el problema difícil de las curvas elípticas:
Tamaño de clave
La gran ventaja de las curvas elípticas en criptografía (EEC) es que nos permiten utilizar criptografía asimétrica con una clave mucho más pequeña
| Simétrica | RSA | D-H ( |
Curvas elípticas |
|---|---|---|---|
| 80 | 1024 | 1024, 160 | 160 |
| 128 | 3072 | 3072, 224 | 256 |
| 192 | 7680 | 7680, 384 | 384 |
| 256 | 15360 | 15360, 512 | 512 |
Es decir, pone la criptografía asimétrica al alcance de pequeños dispositivos
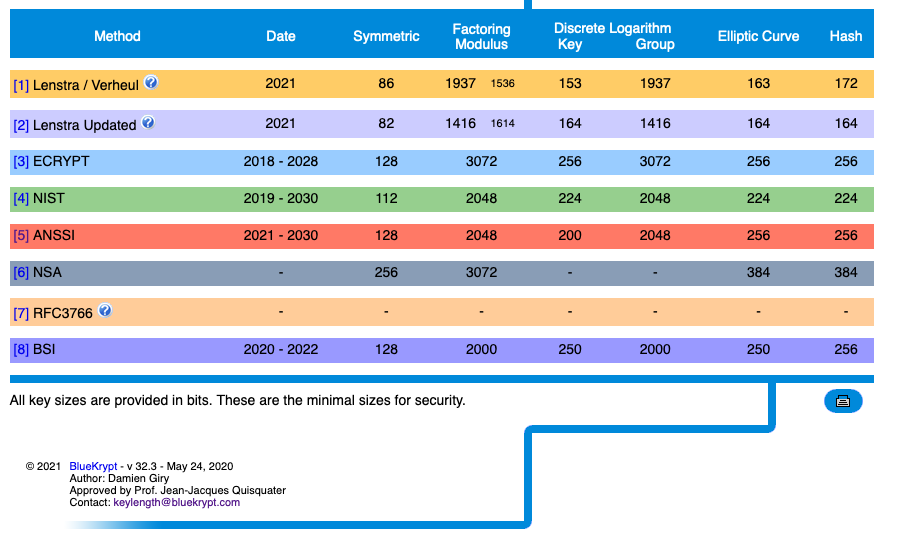
NOTA: RSA está basado en "factorización", DSA y D-H en "logaritmo discreto"
Conclusiones
| Característica | Cifrado simétrico | Cifrado asimétrico |
|---|---|---|
| Eficiencia | Muy rápido | Lento |
| Claves | 1 (secreta, compartida) | 2 (una pública y otra privada) |
| Tamaño de clave | 256 bits | 15360 bits (RSA), 512 bits (curvas elípticas) |
| Servicios | Confidencialidad | Autenticación, integridad, intercambio de claves simétricas (Diffie-Hellman) |
| Ejemplos | AES, ChaCha | RSA, ECDSA, ECDH |
Resumen
- Confidencialidad computacional: hoy en día no es práctico romperla (en 30 años, quizá sí)
- Fortaleza de un algoritmo: "esfuerzo" necesario para romper un sistema. Relacionado con la longitud de la clave.
- Cifrados simétricos: misma clave para cifrar y descifrar
- Cifrado de flujo:
- A partir de una clave corta, generamos un flujo "pseudoaleatorio" tan largo como el mensaje. cifrado y descifrado=
RANDOM XOR MENSAJE. - Ejemplos: RC4 (antiguo), ChaCha20
- A partir de una clave corta, generamos un flujo "pseudoaleatorio" tan largo como el mensaje. cifrado y descifrado=
- Cifrado de bloque:
- Se divide el mensaje en bloques, cada bloque se cifra por separado.
- Es necesario utilizar el modo de funcionamiento adecuado
- Ejemplos: 3DES (no se usa en protocolos modernos), AES
- Cifrado de flujo:
- Es necesario evitar cifrar dos mensajes diferentes con la misma clave
- Criptografía asimétrica: cada persona tiene dos claves, una para cifrar y otra para descifrar. Una de esas claves es pública (es decir, cualquiera puede conocer la clave pública de otra persona) y la otra es secreta
- Muchísimo más lenta que el cifrado simétrico
- Se utiliza para:
- intercambiar claves simétricas (Diffie-Hellman, ECDH)
- firmado e identidad digital (RSA, ECDSA)
- Ejemplos clásicos: RSA, DSA, D-H. Están basados en el problema de la factorización de números primos y logaritmo discreto. Necesitan tamaños de clave grandes y eso dificulta su implementación
- Las curvas elípticas (EC) permite claves mucho más pequeñas = más rápidos
- Ejemplos modernos: ECDH, ECDSA, que son adaptaciones de D-H y DSA sobre curvas elípticas
Referencias
- The Salsa20 family of stream cipher, Daniel J. Bernstein, 2017
- Block Cipher Techniques, NIST
- Recommendation for Key Establishment Using Symmetric Block Ciphers, NIST 800-71, 2018
- Algorithms, key size and parameters report 2014, ENISA, 2014
- Nuevas direcciones en la criptografía Whitfield Diffie y Martin Hellman, 1976
- Asymmetric Encryption - Simply explained
- Diffie-Hellman Key Exchange explained (Python)
Las curvas elípticas son un concepto complejo. Esto son algunas propuestas explicativas:
- ¿Por qué pueden utilizarse las curvas elípticas para cifrar?, píldoras CriptoRED
- Elliptic Curve Cryptography Overview, de John Wagnon. No asume conocimientos de álgebra.
- Elliptic Curve Diffie Hellman: Vídeo sobre ECDH y curvas elípticas en general de Robert Pierce. Asume conocimientos de álgebra.
Ejercicios: https://colab.research.google.com/github/Juanvvc/crypto2/blob/main/ejercicios/02/Sistemas de cifrado.ipynb
Continúa en: Funciones de Hash y firma digital